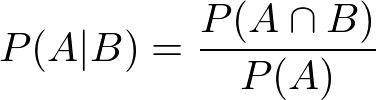【scikit-learn】Ridge回帰【その2】
RidgeCVというモデルがあるらしい.
CVとはCrossVaridationのことで,正則化パラメータαに交差検証を用いる方法である.
これによって最適なαを自動で求めてくれるそう.
reg = linear_model.RidgeCV(alpha= [0.1, 1.0, 10.0]) reg.fit(X_train, y_train) reg.alpha_
でできる.
デフォルトではleave-out-cross-varidation(LOOCV,一個抜き交差検証)で正則化パラメータの候補集合から1つをテスト事例として抜き,残りをトレーニングデータとして使う.
これを全事例が一回ずつテスト事例となるように検証を繰り返す.
【scikit-learn】Ridge回帰
Ridge回帰は係数に対して
を満たす
を見つけるというもの.
Ridge回帰による正則化係数 と係数
と係数 の関係を見てみる
の関係を見てみる
import numpy as np import matplotlib.pyplot as plt import sklearn.linear_model # 10*10の行列を作る X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis]) y = np.ones(10)
Xは
[[ 1 2 3 4 5 6 7 8 9 10] [ 2 3 4 5 6 7 8 9 10 11] [ 3 4 5 6 7 8 9 10 11 12] [ 4 5 6 7 8 9 10 11 12 13] [ 5 6 7 8 9 10 11 12 13 14] [ 6 7 8 9 10 11 12 13 14 15] [ 7 8 9 10 11 12 13 14 15 16] [ 8 9 10 11 12 13 14 15 16 17] [ 9 10 11 12 13 14 15 16 17 18] [10 11 12 13 14 15 16 17 18 19]]
の行列の各要素で1を割った行列なので,左上に行くほど大きく,右下に行くほど小さい値となっている0.5~1.0の行列である.
次に学習を行う.
n_alphas = 200 alphas = np.logspace(-10, -2, n_alphas)#1e-10 ~ 1e-2までを10を底とした指数で表示 coefs = [] for a in alphas: ridge = linear_model.Ridge(alpha=a, fit_intercept=False)#モデルの定義 ridge.fit(X, y)#学習 coefs.append(ridge.coef_)
ridge.fit(X,y)のところは図にするとおそらくこんな感じ.

次にプロットを行う.
ax = plt.gca() ax.plot(alphas, coefs) ax.set_xscale('log') ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis plt.xlabel('alpha') plt.ylabel('weights') plt.title('Ridge coefficients as a function of the regularization') plt.axis('tight') plt.show()
出力結果は下のようになった.

これはあるαのときにおける式1-10の係数wの大きさを表している.
αが小さいとき(グラフの右に行くほど)となるのでこれはほぼ線形回帰であり,係数の影響を抑えきれなくなる.
αが大きいほど(グラフの左に行くほど)wは小さくなりたがろうとするので係数の大きさはほぼ0になる.
【補足】
ベクトルの作り方
a = np.arange(0,10) #[0,1,2,3,4,5,6,7,8,9] b = np.linspace(0,10,6) #[0,2,4,6,8,10] c = np.logspace(2,5,4) #[10**2,10**3,10**4,10**5] d = np.ones(10) #[1,1,1,1,1,1,1,1,1,1] e = np.zeros(10) #[0,0,0,0,0,0,0,0,0,0]
【numpy】行列操作【その1】
numpyの行列操作で面白い行列の作り方を知ったので書く.
a = np.arange(1,11) b = np.arange(0,10) #b: [0,1,2,3,4,5,6,7,8,9] c = b[:,np.newaxis] #c: #[[0] # [1] # [2] # [3] # [4] # [5] # [6] # [7] # [8] # [9]] d = a + c #[[ 1 2 3 4 5 6 7 8 9 10] # [ 2 3 4 5 6 7 8 9 10 11] # [ 3 4 5 6 7 8 9 10 11 12] # [ 4 5 6 7 8 9 10 11 12 13] # [ 5 6 7 8 9 10 11 12 13 14] # [ 6 7 8 9 10 11 12 13 14 15] # [ 7 8 9 10 11 12 13 14 15 16] # [ 8 9 10 11 12 13 14 15 16 17] # [ 9 10 11 12 13 14 15 16 17 18] # [10 11 12 13 14 15 16 17 18 19]] X = 1./ d # 1.をdの要素で割った形
matplotlib.pyplotで一枚の枠に図を複数埋め込む方法
下のように宣言すればよい
plt.figure() plt.subplot(y,x,i)
これは文字列でもできるらしく,scikit-learnの公式documentではこちらの方が使用されていたため,文字列のほうが主流なのか?
plt.subplot(211) plt.subplot(212)
正規分布を作る
numpy.random.randn()は正規分布に従って乱数が生成されるらしい.
今回は
x = numpy.random.randn(発生させる個数)
y = 正規関数(x)
で正規分布の曲線の発生過程を作った.
import matplotlib.pyplot as plt import numpy as np plt.figure() h_length = 4 w_length = 6 for h in range(h_length): for w in range(w_length): i = h*w_length+w+1 fig_loc = str(h_length) + str(w_length) + str(i) plt.subplot(h_length,w_length,i) #グラフプロット #xの個数 num = 10*i x = np.random.randn(num) y = np.exp(-x**2/2)/np.sqrt(2*np.pi) plt.title(num) plt.xlim([-3,3]) plt.ylim([-0.1,0.55]) plt.scatter(x,y,c="green") plt.show()

【scikit-learn】線形回帰
研究で識別/分類問題について実装することになるだろうので,scikit-learnの公式ドキュメント(http://scikit-learn.org/stable/index.html)のうち
classificationを勉強していこうと思う.
今回は線形回帰について(なぜ回帰?)
scikit-learnは
#modelの定義 regression = sklearn.linear_model.LinearRegression() #学習 #定義したモデル.fit(トレーニングデータ, トレーニングデータのラベル) regression.fit(X_train,y_train) #予測 #予測ラベル = 定義したモデル.predict(テストデータ) y_pred = regression.predict(X_test)
という感じでやるらしい.
線形回帰はMSEを最小化するという方法である.
糖尿病患者
diabetesデータセットは
age, sex, bmi, map, tc, ldl, hdl, tch, ltg, gluという10個の属性が入っている.
目的変数は1年後の疾患の進行状況らしい.
これらを線形回帰によって当てはめてみる.
import matplotlib.pyplot as plt import numpy as np from sklearn import datasets from sklearn import linear_model from sklearn.metrics import mean_squared_error from sklearn.metrics import r2_score # load the diabete dataset diabetes = datasets.load_diabetes() categories = {0:"age",1:"sex",2:"bmi",3:"map",4:"tc",5:"ldl",6:"hdl",7:"tch",8:"ltg",9:"glu"} #全体の図を定義 plt.figure() for key,val in categories.items(): print(key) #データをある属性のみに絞る diabetes_X = diabetes.data[:, np.newaxis, key] #データをトレーニングとテストに分割 diabetes_X_train = diabetes_X[:-20] diabetes_X_test = diabetes_X[-20:] #目的変数をトレーニングとテストに分割 diabetes_y_train = diabetes.target[:-20] diabetes_y_test = diabetes.target[-20:] #線形回帰モデルの宣言 regr = linear_model.LinearRegression() #学習 regr.fit(diabetes_X_train,diabetes_y_train) #予測 diabetes_y_pred = regr.predict(diabetes_X_test) #係数 print("Cofficients:\n",regr.coef_) #MSE計算 print("mean squared error:%.2f"%(mean_squared_error(diabetes_y_test,diabetes_y_pred))) #分散 print("Variance score:%.2f"%r2_score(diabetes_y_test,diabetes_y_pred)) #subplot fig_loc = "25" + str(key) plt.subplot(fig_loc) #plot outputs plt.scatter(diabetes_X_test,diabetes_y_test,color="black") plt.plot(diabetes_X_test,diabetes_y_pred,color="blue",linewidth=3) #plt.xticks(()) #plt.yticks(()) plt.title(categories[key]) plt.show()
結果はこのようになった.
sexのような2値に対しては当然ながら線形回帰は使えない.(そもそも使う意味がない.)
bmiやhdl, ltgあたりは割りと線形回帰で良い結果が出た方だと思う.

識別器に意図的に誤分類させる研究
識別器に意図的に誤分類を誘発させる研究の記事を読んだ.
今のプロジェクトが終わったらやってみたいのでメモ.
TeX余白の設定
表や図における余白の設定
【Windows】TeXworksにforestを入れる
dirtreeパッケージよりもforestのほうが綺麗にディレクトリツリーを表示できたのでメモ.
インストールの仕方
forestパッケージのダウンロード
https://www.ctan.org/pkg/forest
https://github.com/sasozivanovic/forest
inlinedefパッケージのダウンロード
forestだけで宣言したらinlinedef.styがないとエラーが出たので依存関係がある
https://www.ctan.org/tex-archive/macros/latex/contrib/inlinedef
TeXの環境を更新
$mktexlsr
サンプル
\usepackage{forest} %forest definition------------------------------------------- \definecolor{folderbg}{RGB}{124,166,198} \definecolor{folderborder}{RGB}{110,144,169} \def\Size{4pt} \tikzset{ folder/.pic={ \filldraw[draw=folderborder,top color=folderbg!50,bottom color=folderbg] (-1.05*\Size,0.2\Size+5pt) rectangle ++(.75*\Size,-0.2\Size-5pt); \filldraw[draw=folderborder,top color=folderbg!50,bottom color=folderbg] (-1.15*\Size,-\Size) rectangle (1.15*\Size,\Size); } } %------------------------------------------- \begin{document} \begin{figure} \begin{forest} for tree={ font=\ttfamily, grow'=0, child anchor=west, parent anchor=south, anchor=west, calign=first, inner xsep=12pt, edge path={ \noexpand\path [draw, \forestoption{edge}] (!u.south west) +(6.5pt,0) |- (.child anchor) pic {folder} \forestoption{edge label}; }, % style for your file node file/.style={edge path={\noexpand\path [draw, \forestoption{edge}] (!u.south west) +(6.5pt,0) |- (.child anchor) \forestoption{edge label};}, inner xsep=2pt,font=\small\ttfamily }, before typesetting nodes={ if n=1 {insert before={[,phantom]}} {} }, fit=band, before computing xy={l=15pt}, } [Project [Sample [sample.py,file] [sample.java,file] ] [img [a.png,file] [b.png,file] ] ] \end{forest} \centering\caption{プロジェクトの構成}\label{Project} \end{figure} \end{document}

WidowsのTeXworksでstyファイルを読み込む
今回はdirtreeというパッケージを入れた.
忘れないようにメモ
TeXの\usepackage{hoge}という宣言ではhoge.styというファイルを読み込んでいる.
最も簡単な方法はそのtexファイルと同じディレクトリに入れることである.
しかしそのプロジェクトのみでしか使えないため不便である.
そこでPATHの設定のようにいつでも使えるように設定した.
1. まずdirtreeファイル一覧をダウンロードする.
https://ctan.org/pkg/dirtree
2. insファイルからstyファイルを生成する
$ platex dirtree.ins
3. TeXworksのフォルダに入れる
自分の場合だとC:\w32tex\share\texmf-dist\tex\latex\0_mypackage\dirtreeというフォルダにファイル一覧を突っ込んだ.
先に読み込まれるほど優先度が高いそうなのでファイル名は0などから始めると良いらしい.
4. 環境を更新
$ mktexlsr
5. 確認
\usepackage{dirtree}
でエラーが出ないか確認
【参考】
http://oku.edu.mie-u.ac.jp/tex/mod/forum/discuss.php?d=454
https://ameblo.jp/masayan24/entry-10360005851.html
http://ocg.aori.u-tokyo.ac.jp/member/daigo/comp/memo/?val=all&typ=all&nbr=0000000170
不均衡データへの対応
正例と負例の数が極端に偏っているデータのことを不均衡データという.
今回はBoW(Bag of Words)でスパムメールの判定をロジスティック回帰で行った.
BoWでは大量の単語の集合のうち, 出現頻度の高い単語のみを残すためサンプル数の多いクラスに影響されてしまう.
例えばスパムメール判定だと, 通常サンプルは正常メールよりスパムメールの数の比率が小さいのでBoWにより圧縮される過程で正常メールに出現する単語が多くなってしまう.
「振り込み」や「年会費無料」みたいな単語はスパムメールに多そうだが, サンプルが正常メール1万件に対してスパムメール100件だと正常メールに現れる単語ばかりに注目しスパムメールの情報を蔑ろにしてしまう.
この対策方法について調べた.
- 不均衡を調整する係数をモデルに導入
- 多数はデータを減少, 少数派データを増加
2番目の方法としてSMOTEアルゴリズムというものがあるらしい.
負例をアンダーサンプリングし, 正例をオーバーサンプリングする手法である.
アンダーサンプリングはランダムに行い, オーバーサンプリングはk-最近傍点までの距離でランダムに生成.
【参考文献】
・http://tjo.hatenablog.com/entry/2014/10/09/224106
・http://d.hatena.ne.jp/sfchaos/20111202/p1
・http://qiita.com/shima_x/items/370587304ef17e7a61b8
【tensorflow】Irisデータセットで線形分離で二値分類
Irisデータセットは特徴量として「萼片の長さ」「萼片の幅」「花びらの長さ」「花びらの幅」が与えられ
ラベルはそれぞれ0:setosa, 1:versicolor, 3:virginicaである.

setosa

versicolor

verginica
このデータセットに対してsetosaとそれ以外の二値分類を行った.
まず使うモジュールをimportし計算グラフを宣言する.
import matplotlib.pyplot as plt import numpy as np from sklearn import datasets import tensorflow as tf sess = tf.Session()
次にIrisデータセットを取得
setosaに1 , それ以外に0を割り当てる.
iris = datasets.load_iris() binary_target = np.array([1. if x==0[f:id:umashika5555:20170907030429p:plain] else 0. for x in iris.target]) iris_2d = np.array([[x[2],x[3]] for x in iris.data])# 花びらの長さと花びらの幅の2つの値の組をデータとする
バッチサイズ, プレースホルダ, 変数を宣言
batch_size = 20 x1_data = tf.placeholder(shape=[None,1], dtype=tf.float32) x2_data = tf.placeholder(shape=[None,1], dtype=tf.float32) y_target = tf.placeholder(shape=[None,1], dtype=tf.float32) A = tf.Variable(tf.random_normal(shape=[1,1])) b = tf.Variable(tf.random_normal(shape=[1,1]))
線形モデルを定義
my_mult = tf.matmul(x2_data,A) my_add = tf.add(my_mult,b) my_output = tf.subtract(x1_data,my_add)
損失関数を定義
xentropy = tf.nn.sigmoid_cross_entropy_with_logits(logits=my_output,labels=y_target)
最適化関数を定義
my_opt = tf.train.GradientDescentOptimizer(0.05)
train_step = my_opt.minimize(xentropy)
変数を初期化する
init = tf.global_variables_initializer() sess.run(init)
線形モデルを1000回のイテレーションでトレーニング
for i in range(1000): rand_index = np.random.choice(len(iris_2d),size=batch_size) rand_x = iris_2d[rand_index] rand_x1 = np.array([[x[0]] for x in rand_x]) rand_x2 = np.array([[x[1]] for x in rand_x]) rand_y = np.array([[y] for y in binary_target[rand_index]]) sess.run(train_step,feed_dict={x1_data:rand_x1, x2_data:rand_x2, y_target:rand_y}) if (i+1)%200==0: print("step #", str(i+1) + "A=" + str(sess.run(A)) + ", b= " + str(sess.run(b)))
実行結果
step # 200A=[[-2.14318705]], b= [[ 8.48896122]] step # 400A=[[-3.59071422]], b= [[ 10.84847546]] step # 600A=[[-4.73809004]], b= [[ 12.31665611]] step # 800A=[[-5.16311646]], b= [[ 13.66902447]] step # 1000A=[[-5.86469412]], b= [[ 14.52292442]]
結果をグラフにプロットする.
[[slope]] = sess.run(A) [[intercept]] = sess.run(b) x = np.linspace(0,3,num=50) ablineValues = [] for i in x: ablineValues.append(slope*i+intercept) setosa_x = [a[1] for i,a in enumerate(iris_2d) if binary_target[i] == 1] setosa_y = [a[0] for i,a in enumerate(iris_2d) if binary_target[i] == 1] non_setosa_x = [a[1] for i,a in enumerate(iris_2d) if binary_target[i] == 0] non_setosa_y = [a[0] for i,a in enumerate(iris_2d) if binary_target[i] == 0] plt.plot(setosa_x,setosa_y,"rx",ms=10, mew=2, label="setosa") plt.plot(non_setosa_x,non_setosa_y,"ro",label="NOn setosa") plt.plot(x,ablineValues) plt.xlim([0.0,2.7]) plt.ylim([0.0,7.1]) plt.suptitle("Linear Separator For I.setosa") plt.xlabel("Petal Length") plt.ylabel("Petal Width") plt.legend(loc="lower right") plt.show()

これは線形分離でx1[None*1] - (x2[None*1]*A[1*1] + b[1*1]) = 0[1*1]という直線の下か上かで種類を判別する方法である.
この場合線形分離可能なモデルなので綺麗に分離できたがsetosa以外を分類しようとすると上手くいかない.

versicolorを分類しようとした場合

versinicaを分類しようとした場合
線形分離可能なデータに対しては上手く働くが, それ以外のものに関しては上手く行かないことが分かる.
むしろ現実世界では線形分離不可能なもののほうが多いのでそれらに対処していく必要がある.
今後SVMやNNの記事を書いていく.
League of Legendsのチャンプ間の分析
pythonのライブラリnetworkxの勉強がてらにLeague of Legends(以後LoL)におけるチャンピオン間のネットワークを作った.
LoLとは世界的に人気のオンラインゲームであり,全10人のプレイヤーが5人,5人に分かれて戦い合う.
下のようなマップで相手の陣地の一番奥にあるオブジェクトを最初に壊したチームが勝利である.

下の動画はLoLのプロゲームで私が最も好きな試合である.
www.youtube.com
LoLでは始め, レーン戦と呼ばれるtop,midと呼ばれる2つのレーンで1on1を行う.
またbotというレーンでは火力が高いが体力が低いadcという役職のプレイヤーと火力は低いが回復やシールド能力のあるsupという役職が2on2で戦う.
jungleというレーンは中間モンスターと呼ばれる,相手プレイヤーとは直接関係のないモンスターを狩り経験値を高めつつ,味方のレーンを補助しにいったりする.
このとき,レーン戦ではチャンピオンによって対面が得意, 不得意がある.
あるチャンピオンに対して, そのチャンピオンに有利なチャンピオンをカウンターチャンプという.
例えばAnnieというチャンピオンはmidレーンにおいて火力は高いのだが, 射程はかなり短い. したがって射程の長いBrandやOriannna,Luxといったチャンプに弱い. 逆に射程の短いFizzやAkaliといったチャンプに対しては非常に有利である.
カウンターチャンプの概念はかなり重要でプロの試合でもチャンピオンピックの時点で有利不利が決まらないように工夫されている.
__________________________________________________
まずはJSONファイルの取得からする必要がある.
LoL Counter - Champions
今回はこのサイトからスクレイピングした.
(スクレイピングのやり方についてはいつか記載)
JSONファイルはここにおいてある.
champion1.json - Google ドライブ
赤線が不得意チャンプ, 青線が得意チャンプ, 緑線が味方で相性の良いチャンプ
import json import matplotlib.pyplot as plt import networkx as nx def get_champion_relations_dict(): """JSONファイルを取得 """ with open("champion.json","r") as f: return json.load(f) def add_edges(Graph,champion_name,tmp_list,edge_color): """チャンピオンに対してtmp_listのチャンピオンに対するエッジを追加する """ Graph.add_edges_from([(champion_name,champion) for champion in tmp_list],color=edge_color) if __name__ == "__main__": #有向グラフを宣言 Graph = nx.DiGraph() #チャンピオンのJSONを取得 champion_relations_dict = get_champion_relations_dict() #ノードを追加する Graph.add_nodes_from(list(champion_relations_dict.keys())) #カウンターチャンピオンに有向エッジを追加 relations_dict = {"weak":"r","strong":"b","goes_well":"g"} for champion_name in champion_relations_dict.keys():#あるチャンピオンに対して for relation,color in relations_dict.items():#ある関係に対して opponent_list = champion_relations_dict[champion_name][relation][:3] add_edges(Graph,champion_name,opponent_list,color) #グラフの描画 edges = Graph.edges() colors = [Graph[u][v]["color"] for u,v in edges] plt.figure(figsize=(50,50)) pos = nx.spring_layout(Graph) labels=nx.draw_networkx_labels(Graph,pos=nx.spring_layout(Graph)) nx.draw_networkx(Graph,pos,edge_color=colors,node_color="w",alpha=0.5,edge_labels=labels,font_size=9) plt.axis("off") plt.savefig("default.png") plt.show()
結果はいろいろ調整して以下のようになった.




正直, かなり見づらいしノードが多いため目的のチャンプを探すのに時間がかかる.
またノードの◯が表示されない場所があるのはライブラリの関係なのだろうか?
あと, グラフのノードの散乱をpos = nx.spring_layout(Graph,k=0.7)のように反発係数でやる以外に方法はないのか?
凡例の表示をどうするか?などの問題を解決していけたらよい.
これらを直せたら直していきたい.
【参考にしたサイト】
本家
https://networkx.github.io/documentation/networkx-1.9/examples/drawing/labels_and_colors.html
https://networkx.github.io/documentation/networkx-1.10/reference/functions.html
stack overflow
https://stackoverflow.com/questions/25639169/networkx-change-color-width-according-to-edge-attributes-inconsistent-result
https://stackoverflow.com/questions/24873626/python-networkx-adding-color-for-a-particular-edge
https://stackoverflow.com/questions/22992009/legend-in-python-networkx
Qiita
http://qiita.com/hitsumabushi845/items/270d81c5c8017014df95
http://qiita.com/inoory/items/088f719f2fd9a2ea4ee5
http://qiita.com/hatchinee/items/a904c1f8d732a4686c9d
Python辞書について
http://www.yukun.info/blog/2008/06/python-dict2.html
DeepLearning実装 #1
名著『ゼロから作るDeepLearning』を読み終わったので特に重要であった4,5,6,7章について4回に渡って解説をしたいと思う.
第1回目は4章の「ニューラルネットワークの学習」である.
4.1 データから学習する
ニューラルネットワークは他の機械学習の手法と違ってデータから学習できるというのが特徴.
すなわち重みパラメータの値をデータから自動で決定できる.
例えば手書き文字の認識を行いたいとき機械学習は人間が決めた「角がいくつあるか?」「横線がいくつあるか?」などの特徴量を抽出する.
しかしニューラルネットワークではその過程を自動でやってくれるため, 手書き文字の画像を突っ込めばよいだけである.
4.2 損失関数
2乗和誤差や交差エントロピー誤差がよく用いられる.
交差エントロピー誤差とはで表されます.
ここではone-hot-vectorなのでEは実質的に正解ラベルのものの確率の対数にマイナスをつけたものである.
例えば正解ラベルが「2」のときt = numpy.array([0,0,1,0,0,0,0,0,0,0])となっておりならば
となる.

上図はのグラフである. xが1に近づくほど(入力手書き文字画像が「2」である確率が1に近づくと)損失が少ないということがわかる.
ここでミニバッチ学習を適用すると損失関数は「バッチすべてのデータにおける訓練データ1つあたりの損失」となるので損失関数の定義は
となる.
ミニバッチをランダムに取り出すときのテクニックとしてランダムに選ぶ方法がある.
#0-60000未満の数字の中からランダムに10個の数字を選ぶ np.random.choice(60000,10)
バッチに対応した交差エントロピー誤差の実装として
正解ラベルがone-hot-vectorの場合とargmax(one-hot-vector)の2つの場合が考えられる.
どちらでも対応出来るように処理を書くと下のようになる.
def cross_entropy_error(y, t): """損失関数:クロスエントロピー誤差""" if y.ndim == 1: t = t.reshape(1, t.size) y = y.reshape(1, y.size) # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換 if t.size == y.size: t = t.argmax(axis=1) batch_size = y.shape[0] return -np.sum(np.log(y[np.arange(batch_size), t])) / batch_size
4.3 数値微分
損失関数を小さくするために勾配の情報を用いる.
勾配を得るために数値微分が必要となる.
微分の定義はである.
Pythonで実装する際にこのhは十分に小さい値だからといって1e-50などを選択してはいけない.
なぜなら丸め誤差の影響で計算機上では0と同値であるからである.
数値微分の誤差を減らす工夫として(x+h)と(x-h)での関数fの差分を計算して
より
def numeric_diff(f,x): h = 1e-4 return (f(x+h)-f(x-h))/(2*h)
次に勾配法について説明する.
各地点において関数の値を最も減らす方向を示すのが勾配.
勾配が指す先は関数が小さくなる方向ではあるが関数の最小値とは限らないのが注意.
入力がとすると勾配法は
は学習率
関数の勾配がわかったところでニューラルネットワークに適用する.
すなわち行列式における勾配を求める.
ニューラルネットワークの重みをWとすると
\begin{equation}W= \begin{pmatrix}w_{11} &w_{12}\\ a_{21} &a_{22}\end{pmatrix}\end{equation}
ここで損失関数LをWで微分すると
\begin{equation}\frac{\partial L}{\partial W} = \begin{pmatrix}\frac{\partial L}{\partial w_{11}} &\frac{\partial L}{\partial w_{12}}\\ \frac{\partial L}{\partial w_{21}} &\frac{\partial L}{\partial w_{22}}\end{pmatrix}\end{equation}
というように各要素でLを偏微分する.
数値微分を用いた2層ニューラルネットワークを実装する.
class TwoLayerNet: def __init__(self,input_size,hidden_size,output_size,weight_init_std=0.01): self.params = {} self.params["W1"] = weight_init_std * np.random.randn(input_size,hidden_size) self.params["b1"] = np.zeros(hidden_size) self.params["W2"] = weight_init_std*np.random.randn(hidden_size,output_size) self.params["b2"] = np.zeros(output_size) def predict(self,x): W1,W2 = self.params["W1"],self.params["W2"] b1,b2 = self.params["b1"],self.params["b2"] a1 = np.dot(x,W1) + b1 z1 = sigmoid(a1) a2 = np.dot(z1,W2) + b2 y = softmax(a2) return y #x:入力データ, t:教師データ def loss(self,x,t): y = self.predict(x) return cross_entropy_error(y,t) def accuracy(self,x,t): y = predict(x) y = np.argmax(y,axis=1) t = np.argmax(t,axis=1) accuracy = np.sum(y == t)/float(x.shape[0]) def numerical_gradient(self,x,t): loss_W = lambda W:self.loss(x,t) grads = {} grads["W1"] = numerical_gradient(loss_W,self.params["W1"]) grads["b1"] = numerical_gradient(loss_W,self.params["b1"]) grads["W2"] = numerical_gradient(loss_W,self.params["W2"]) grads["b2"] = numerical_gradient(loss_W,self.params["b2"]) return grads
MNISTデータセットをダウンロードしてトレーニングする.
#MNISTのインストール train_loss_list = [] iters_num = 10000 train_size = x_train.shape[0] batch_size = 100 learning_rate = 0.1 network = TwoLayerNet(input_size=784,hidden_size=50,output_size=10) for i in range(iters_num): #ミニバッチの取得 batch_mask = np.random.choice(train_size,batch_size) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] #勾配の計算 grad = network.numerical_radient(x_batch,t_batch) #パラメータの更新 for key in ("W1","b1","W2","b2"): network.params[key] -= learning_rate*grad[key] #学習経過の記録 loss = network.loss(x_batch,t_batch) train_loss_list.append(loss)
これにテストをして精度を見る.
精度に関しては次の章で改めて書くと思うので省略.
教師あり学習分類問題の決定境界の可視化
パーセプトロン,SVM,ロジスティック回帰,ランダムフォレストなど「決定境界を求める」という分類問題を解く際に下のような2次元グラフで決定境界を可視化できると嬉しい.
今回は決定境界を引くアルゴリズムをまとめた.

手順は以下の通りである.
- 学習モデルでサンプルを分類する.
- 2Dグラフの軸の範囲を決める
- 2Dグラフ上にグリッドポイントを作成する
- グリッドポイント全てに対して学習モデルを適用
- グリッポポイントの等高線のプロット
1. 学習モデルでサンプルを分類する
今回はIrisデータセットからガクの長さ, 花弁の長さを特徴量として用いる.
http://www.geocities.jp/umashika_ningen/blog1.html
現在下記のような状態(サンプルとそのラベルはわかっている.)

ここで学習モデルをサンプルに適用し, 決定境界を求める.
学習によって得られた境界線をy = WX + bと数式を得ることができる.
2. 2Dグラフの軸の範囲を決める
まずサンプルの中で最も大きい値と小さい値をみてそれにフィットするようなグラフの範囲を決める.
特徴量の変数がXとすると
x1_min , x1_max = X[:,0].min()-1, X[:,0].max()+1 x2_min , x2_max = X[:,1].min()-1, X[:,1].max()+1
というように最小値-1,最大値+1を軸の範囲にする.
3. 2Dグラフ上にグリッドポイントを作成する
グラフ上に格子点を打つ.
resolution = 0.02
xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution),np.arange(x2_min,x2_max,resolution))
4. グリッドポイント全てに学習モデルを適用
1.の時点で境界線は引けているわけなので各グリッドポイントに対して予測のみをすれば良い.
#classifierは学習したモデル #各特徴量を1次元配列に変換して予測を実行 Z=classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
5. グリッポポイントの等高線のプロット
決定境界をプロットする.
form matplotlib.pyplot as plt #予測結果を元のグリッドポイントのデータサイズに変換 Z=Z.reshape(xx1.shape) #グリッドポイントの等高線のプロット plt.contourf(xx1,xx2,Z,alpha=0.4)